How Do Coefficients Of Model Change With Sample Size
Using a sample to estimate the backdrop of an unabridged population is mutual practice in statistics. For case, the mean from a random sample estimates that parameter for an entire population. In linear regression analysis, we're used to the idea that the regression coefficients are estimates of the true parameters. All the same, it'due south piece of cake to forget that R-squared (Rtwo) is besides an estimate. Unfortunately, it has a problem that many other estimates don't have. R-squared is inherently biased! In this post, I await at how to obtain an unbiased and reasonably precise estimate of the population R-squared. I also present power and sample size guidelines for regression analysis. R-squared measures the force of the relationship between the predictors and response. The R-squared in your regression output is a biased estimate based on your sample. R-squared is like the cleaved bathroom scale: it is deceptively large. Researchers take long recognized that regression's optimization process takes reward of take chances correlations in the sample data and inflates the R-squared. This bias is a reason why some practitioners don't use R-squared at all—it tends to be wrong. What should we do about this bias? Fortunately, in that location is a solution and you're probably already familiar with it: adjusted R-squared. I've written about using the adjusted R-squared to compare regression models with a different number of terms. Some other use is that it is an unbiased figurer of the population R-squared. Adjusted R-squared does what you'd exercise with that cleaved bathroom scale. If you knew the calibration was consistently besides loftier, you'd reduce information technology past an appropriate amount to produce an accurate weight. In statistics this is chosen shrinkage. (YouSeinfeld fans are probably giggling now. Yes, George, we're talking about shrinkage, only here it's a good thing!) Nosotros need to shrink the R-squared down so that it is not biased. Adjusted R-squared does this by comparing the sample size to the number of terms in your regression model. Regression models that have many samples per term produce a improve R-squared guess and require less shrinkage. Conversely, models that take few samples per term crave more shrinkage to correct the bias. The graph shows greater shrinkage when you accept a smaller sample size per term and lower R-squared values. Now that nosotros accept an unbiased estimator, permit's have a look at the precision. Estimates in statistics have both a indicate estimate and a confidence interval. For example, the sample hateful is the indicate guess for the population mean. However, the population hateful is unlikely to exactly equal the sample mean. A confidence interval provides a range of values that is likely to contain the population mean. Narrower confidence intervals bespeak a more precise estimate of the parameter. Larger sample sizes help produce more precise estimates. All of this is true with the adjusted R-squared also because it is just another estimate. The adjusted R-squared value is the signal guess, but how precise is it and what's a skillful sample size? Rob Kelly, a senior statistician at Minitab, was asked to written report this issue in social club to develop power and sample size guidelines for regression in the Assistant menu. He simulated the distribution of adjusted R-squared values around different population values of R-squared for different sample sizes. This histogram shows the distribution of 10,000 fake adjusted R-squared values for a true population value of 0.6 (rho-sq (adj)) for a unproblematic regression model. With xv observations, the adjusted R-squared varies widely around the population value. Increasing the sample size from 15 to 40 profoundly reduces the likely magnitude of the difference. With a sample size of xl observations for a simple regression model, the margin of mistake for a 90% conviction interval is +/- xx%. For multiple regression models, the sample size guidelines increment equally yous add terms to the model. These guidelines assist ensure that you have sufficient power to discover a relationship and provide a reasonably precise estimate of the strength of that human relationship. Specifically, if you follow these guidelines: Terms Full sample size 1-3 40 iv-half dozen 45 seven-viii l 9-11 55 12-14 sixty 15-18 65 19-21 70 In closing, if you want to judge the strength of the relationship in the population, assess the adjusted R-squared and consider the precision of the estimate. Fifty-fifty when you meet the sample size guidelines for regression, the adapted R-squared is a rough judge. If the adjusted Rtwo in your output is 60%, you can exist ninety% confident that the population value is between 40-80%. If you're learning about regression, read my regression tutorial! For more histograms and the full guidelines table, see the simple regression white paper and multiple regression white paper.R-squared every bit a Biased Estimate
R-squared Shrinkage
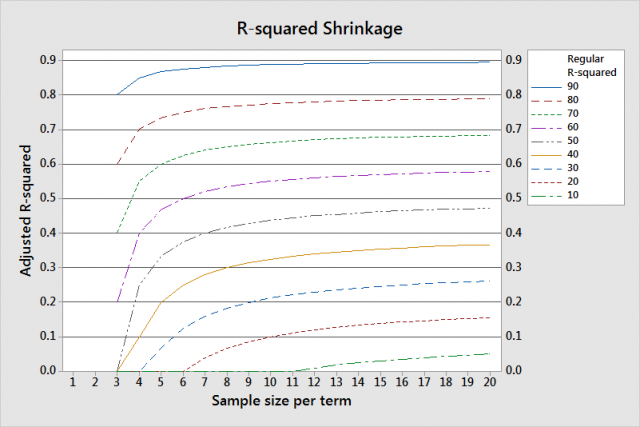
Precision of the Adjusted R-squared Estimate
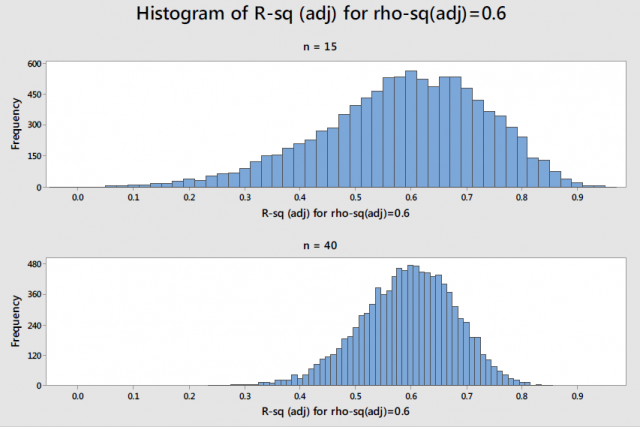
Ability and Sample Size Guidelines for Regression Analysis
How Do Coefficients Of Model Change With Sample Size,
Source: https://blog.minitab.com/en/adventures-in-statistics-2/r-squared-shrinkage-and-power-and-sample-size-guidelines-for-regression-analysis
Posted by: wallingwitheave1948.blogspot.com


0 Response to "How Do Coefficients Of Model Change With Sample Size"
Post a Comment